Commençons cette section par quelques illustrations :












Ces images ne sont pas issues de l'imagination d'un quelconque artiste. Elles ont été générées informatiquement à partir d'une même formule mathématiques. Elles appartiennent à ce qu'on appelle les ensembles de Julia. (Julia est un mathématicien qui leur a donné son nom.)

Voici, sans plus tarder, la formule mathématique qui nous a conduit juste là :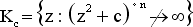



Il s'agit donc de l'ensemble des qui, restent bornés avec l'itératio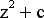n , pour un donné. On parle pour l'ensemble de ces du plan dynamique et pour l'ensemble des du plan des paramètres.

Ce qui est appelé "ensemble de Julia" est la frontière de l'ensemble .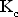

Ces ensembles de Julia sont fractals, c'est-à-dire que l'on peut agrandir une partie de la figure, on obtiendra alors une image du même type.

Les exemples présentés ci-dessus nous montrent des ensembles de Julia connexes. Il en existe qui ne le sont pas :







On peut constater une différence de taille entre les ensembles connexes et ceux qui ne le sont pas : il s'agit de l'origine. Elle appartient aux ensembles connexes, et n'appartient pas aux ensembles non connexes. Il s'agit là d'une des propriétés des ensembles de Julia. Pourquoi est-ce que l'origine est-elle si importante ? En réalité, il s'agit du seul point où la dérivée de la fonction 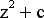s'annule.

On est en mesure de construire un ensemble fournissant les paramètres pour lesquels les ensembles de Julia sont connexes. Il s'agit de l'ensemble de Mandelbrot, construit à partir de la formule suivante :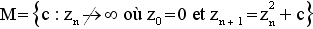



Cet ensemble de Mandelbrot est encore une fractale, comme l'illustre cette figure, construite algorithmiquement :