Les fractales ont pour la plupart un périmètre infini pour une surface finie.

Prenons un exemple, le Flocon de Von Koch :

Le flocon de Von Koch est une fractale connue de tout le monde mathématique. Créée par le mathématicien Helge Von Koch, sa construction est simple à comprendre, et grâce à cette fractale, nous aborderons ultérieurement la notion de dimension fractale.

Etudions sa construction :

Comme dans toute fractale, on retrouve un initiateur et un générateur. Un initiateur est la forme à partir de laquelle on démarre les itérations. Un générateur est la transformation que l'on applique à l'initiateur. Dans notre cas, la transformation consistera à remplacer le tiers central de chaque segment par un triangle équilatéral sans base :



Répétons cette itération plusieurs foi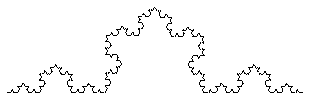s :



On se rend bien compte qu'au bout de 4 itérations, on obtient déjà une figure qui semble compliquée, alors que le système de construction est extrêmement facile à comprendre. Dans ce graphe, on prend de suite conscience de l'autosimilarité propre aux fractales puisque si nous zoomons sur une des pointes du flocon central nous retrouverons systématiquement d'autres flocons identiques au premier.

Le nom de flocon vient du graphe obtenu à partir du moment où on commence les itérations sur un triangle équilatéral. En effet, après plusieurs itérations nous obtenons la figure suivante représentant un flocon de neige :



Cette fractale possède de nombreuses propriétés, mais nous nous concentrerons sur celles relatives à l'étude et la compréhension de la construction des fractales : un périmètre infini pour une aire finie.

On considère le flocon de Von Koch au bout de n itérations.

Soit le nombre de côtés. On a .
Soit la longueur d'un côté. On prend 1 pour mesure du premier côté.

Soit le périmètre du flocon.
donc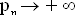

Le flocon de Von Koch a donc un périmètre infini.



On note l'aire du flocon au bout de n itérations. On démontre facilement qu'un triangle équilatéral de base a a pour aire .

La suite 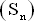est donc définie par :



On va maintenant exprimer en fonction de n pour pouvoir déterminer la limite de la suite :



On a donc .

Le flocon de Von Koch a donc une aire finie.

Une question se pose suite à ce résultat. En effet, nous avons un objet mathématique possédant un périmètre infini et une aire finie. Représenté dans le plan, on pourrait penser que sa dimension est inférieure à 2, mais le fait que son périmètre soit infini nous fait penser qu'elle est supérieure à 1. Etudions donc la dimension fractale.